Getting started with Maxima in Fedora Linux

Maxima is an open source computer algebra system (CAS) with powerful symbolic, numerical, and graphical capabilities. You can perform matrix operations, differentiation, integration, solve ordinary differential equations as well as plot functions and data in two and three dimensions. As such, it is helpful for anyone interested in science and math. This article goes through installing and using Maxima in Fedora Linux.

Installing Maxima

Maxima is a command line system. You can install Maxima from the official Fedora repository using the following command:

sudo dnf install maxima

You can then use Maxima from the terminal by invoking the command maxima.

Installing wxMaxima

wxMaxima is a document based interface for Maxima. To install it in Fedora Linux, use the following command:

sudo dnf install wxmaxima

You can launch wxMaxima either by invoking the command wxmaxima in the terminal or clicking its application icon from the app grid or menu.

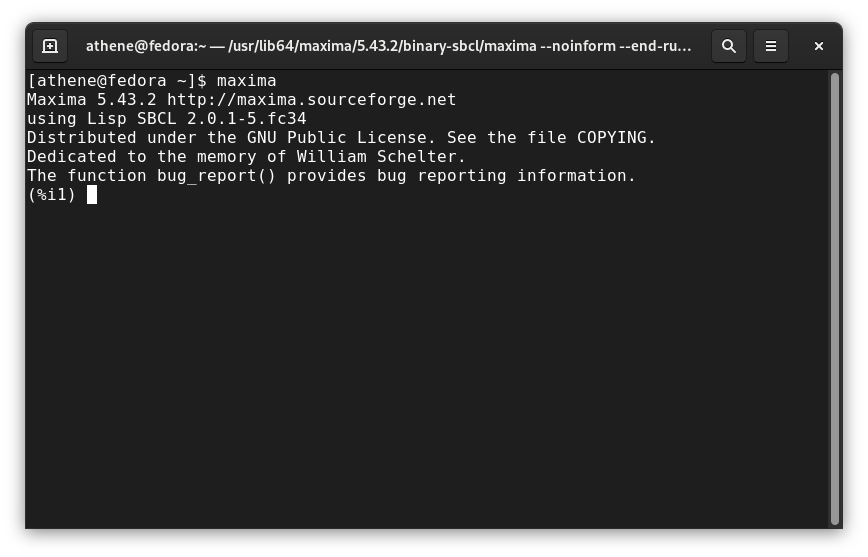
Basic Commands

After calling maxima, you should see terminal output as in the figure above.

The (%i1) is the input label where you enter the commands. Command in Maxima is an expression that can span over many lines and is closed with a semicolon (;). The o labels denote the outputs. Comments are enclosed between /* and */. You can use the special symbol percent (%) to refer to the immediately preceding result computed by Maxima. If you don’t want to print a result, you can finish your command with $ instead of ;. Here are basic arithmetic commands in Maxima:

 (%i1) (19 + 7)/(52 - 2 * 13);
 (%o1)                                  1
 (%i2) 127 / 5;
                                       127
 (%o2)                                 ---
                                        5
 (%i3) float (127 / 5); 
 (%o3)                                25.4
 (%i4) 127.0 / 5;     
 (%o4)                                25.4
 (%i5) sqrt(2.0);
 (%o5)                          1.414213562373095
 (%i6) sin(%pi/2);
 (%o6)                                 1
 (%i7) abs(-12);
 (%o7)                                12
 (%i8) 2+3*%i + 5 - 4*%i;             /*complex arithmetic*/
 (%o8)                              7 - %i

To end the Maxima session, type the command:

quit();

Algebra

Maxima can expand and factor polynomials:

(%i1) (x+y)^3 + (x+y)^2 + (x+y);
                                3          2
(%o1)                    (y + x)  + (y + x)  + y + x
(%i2) expand(%);
          3        2    2      2                  3    2
(%o2)    y  + 3 x y  + y  + 3 x  y + 2 x y + y + x  + x  + x
(%i3) factor(%);
                          2                2
(%o3)           (y + x) (y  + 2 x y + y + x  + x + 1)

To substitute y with z and x with 5, refer the output label above and use the following command:

(%i4) %o3, y=z, x=5;
                                    2
(%o4)                     (z + 5) (z  + 11 z + 31)

You can easily manipulate trigonometric identities:

(%i1) sin(x) * cos(x+y)^2;
                                       2
(%o1)                        sin(x) cos (y + x)
(%i2) trigexpand(%);
                                                         2
(%o2)              sin(x) (cos(x) cos(y) - sin(x) sin(y))
(%i3) trigreduce(%o1);
                   sin(2 y + 3 x) - sin(2 y + x)   sin(x)
(%o3)              ----------------------------- + ------
                                 4                   2

You can also solve algebraic equations in one or more variables:

(%i1) solve(x^2+5*x+6);
 (%o1)                         [x = - 3, x = - 2]
(%i2) solve(x^3 + 1);
                  sqrt(3) %i - 1      sqrt(3) %i + 1
 (%o2)     [x = - --------------, x = --------------, x = - 1]
                        2                   2
(%i3) eqns: [x^2 + y^2 = 9, x + y = 3];
                              2    2
 (%o3)                      [y  + x  = 9, y + x = 3]
 (%i4) solve(eqns, [x,y]);
 (%o4)                 [[x = 3, y = 0], [x = 0, y = 3]]

Calculus

Define f to be a function of x. You can then find the limit, derivative and integral of the function:

(%i1) f: x^2;
                                       2
 (%o1)                                x
 (%i2) limit(f,x,0);
 (%o2)                                  0
 (%i3) limit(1/f,x,0);
 (%o3)                                 inf
 (%i4) diff(f, x);
 (%o4)                                2 x
 (%i5) integrate(f, x);
                                       3
                                      x
 (%o5)                                --
                                      3

To find definite integrals, slightly modify the syntax above.

 (%i6) integrate(f, x, 1, inf);
 defint: integral is divergent.
  -- an error. To debug this try: debugmode(true);
 (%i7) integrate(1/f, x, 1, inf);
 (%o7)                                 1

Maxima can perform Taylor expansion. Here’s the Taylor expansion of sin(x) up to order 5 terms.

(%i1) taylor(sin(x), x, 0, 5);
                                   3    5
                                  x    x
 (%o1)/T/                     x - -- + --- + . . .
                                  6    120

To represent derivatives in unevaluated form, use the following syntax.

(%i2) 'diff(y,x);
                                       dy
 (%o2)                                 --
                                       dx

The ode2 function can solve first and second order ordinary differential equations (ODEs).

(%i1) 'diff(y,x,2) + y = 0;
                                    2
                                   d y
 (%o1)                             --- + y = 0
                                     2
                                   dx
 (%i2) ode2(%o1,y,x);
 (%o2)                     y = %k1 sin(x) + %k2 cos(x)

Matrix Operations

To enter a matrix, use the entermatrix function. Here’s an example of a general 2×2 matrix.

(%i1) A: entermatrix(2,2);
 Is the matrix  1. Diagonal  2. Symmetric  3. Antisymmetric  4. General
 Answer 1, 2, 3 or 4 : 
 4;
 Row 1 Column 1: 
 1;
 Row 1 Column 2: 
 2;
 Row 2 Column 1: 
 3;
 Row 2 Column 2: 
 4;
 Matrix entered.
                                    [ 1  2 ]
 (%o1)                              [      ]
                                    [ 3  4 ]

You can then find the determinant, transpose, inverse, eigenvalues and eigenvectors of the matrix.

(%i2) determinant(A);
 (%o2)                                 - 2
 (%i3) transpose(A);
                                    [ 1  3 ]
 (%o3)                              [      ]
                                    [ 2  4 ]
(%i4) invert(A);
                                  [ - 2   1  ]
                                  [          ]
 (%o4)                            [  3     1 ]
                                  [  -   - - ]
                                  [  2     2 ]
(%i5) eigenvectors(A);
            sqrt(33) - 5  sqrt(33) + 5
 (%o5) [[[- ------------, ------------], [1, 1]], 
                 2             2
               sqrt(33) - 3         sqrt(33) + 3
       [[[1, - ------------]], [[1, ------------]]]]
                    4                    4

In the output label (%o5) the first array gives the eigenvalues, the second array gives the multiplicity of the respective eigenvalues, and the next two arrays give the corresponding eigenvectors of the matrix A.

Plotting

Maxima can use either Gnuplot, Xmaxima or Geomview as graphics program. Maxima package in Fedora Linux comes with gnuplot as a dependency, so Maxima uses gnuplot_pipes as the plotting format. To check the plotting format, use the following command inside Maxima.

get_plot_option(plot_format);

Below are some plotting examples.

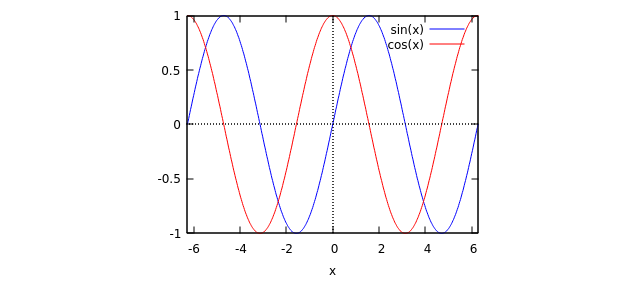
(%i1) plot2d([sin(x), cos(x)], [x, -2*%pi, 2*%pi]);

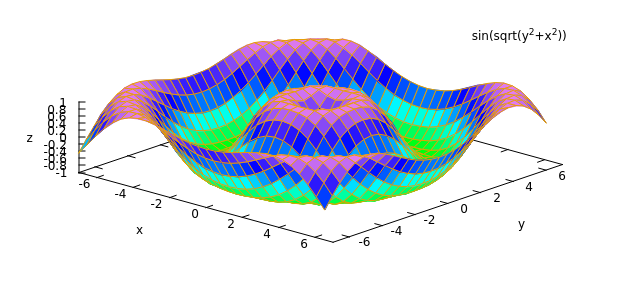
(%i2) plot3d(sin(sqrt(x^2+y^2)), [x, -7, 7], [y, -7, 7]);

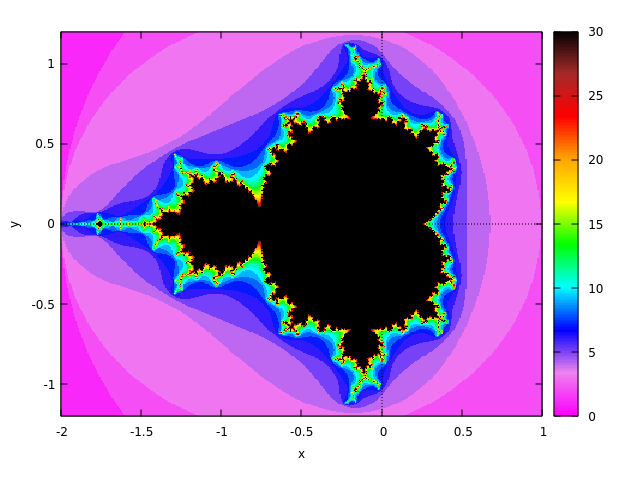
(%i3) mandelbrot ([iterations, 30], [x, -2, 1], [y, -1.2, 1.2],
             [grid,400,400]);

You can read more about Maxima and its capabilities in its official website and documentation.

Fedora Linux has plethora of tools for scientific use. You can find the widely used ones in the Fedora Scientific Guide.